Solved Example on Number System Set-I (Decima to Binary, Octal, Hexadecimal conversion)

As you know decimal, binary, octal and hexadecimal number systems are positional value number systems. To convert binary, octal and hexadecimal to decimal number, we just need to add the product of each digit with its positional value. Here we are going to learn other conversion among these number systems.

Decimal to Binary

Decimal numbers can be converted to binary by repeated division of the number by 2 while recording the remainder. Let’s take an example to see how this happens.

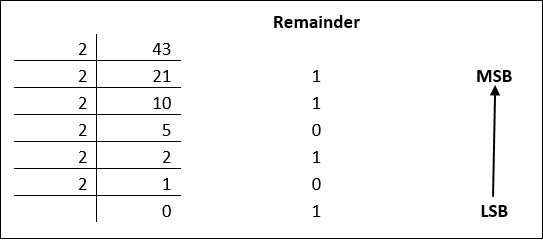
The remainders are to be read from bottom to top to obtain the binary equivalent.

43₁₀ = 101011₂

Decimal to Octal

Decimal numbers can be converted to octal by repeated division of the number by 8 while recording the remainder. Let’s take an example to see how this happens.

Reading the remainders from bottom to top,

473₁₀ = 731₈

Decimal to Hexadecimal

Decimal numbers can be converted to octal by repeated division of the number by 16 while recording the remainder. Let’s take an example to see how this happens.

Reading the remainders from bottom to top we get,

 423₁₀ = 1A7₁₆

 

Here you find step by step process of fractional number conversion to any other number systems. It is very easy to do with some specified steps those are

• We have to multiply the fractional number by base to which number system we want to convert, until the all fractional part is remove/zero.
• Every time we have to take the integer value (before point) after every multiplication, until the all fractional part is remove/zero.
• Then the column of this integer value is read in forward order. That means we have to count those reminder from top to button.

Now take an example to understand the process easily.

Let we have to convert 0.25 decimal numbers to binary number system.

As we discuss above that we have to multiply the fractional number by base to which number system we want to convert. So here we convert the fractional number in binary so we have to multiply by 2.

Now see that process

0.25 x 2 = 0.50   0

0.50 x 2 =1.00     1

See in time of second multiplication the fractional part is remove/zero. So we stop our multiplication and take the column of integer value written in right hand side from top to button.

So equivalent of .2510 is 0.012.

Now if we convert this same number 0.2510 in octal number then we have to multiply with 8.Because the base of octal number is 8.

0.25 x 8 = 2.00        2

So equivalent of .2510 is 0.28.

Now if we convert this same number 0.2510 in Hexadecimal number then we have to multiply with 16.Because the base of octal number is 16.

0.25 x 16 = 4.00 4

So equivalent of .2510 is 0.416.